Расчет наклона линии линейной регрессии с помощью функции НАКЛОН и диаграммы

Наклон линии линейной регрессии выражает наилучшее предсказание зависимой переменной (Y) по независимым перемен­ным (X).

Это цифра, означающая уровень корреляции переменных X и Y. Грубо говоря, с помощью этого мы можем понять как изменится зависимая переменная, если мы поменяем независимую.

Всего в Excel есть два метода нахождения этой переменной.

• С помощью функции НАКЛОН;
• С помощью диаграммы.

В этой статье я продемонстрирую вам оба этих способа.

Что такое наклон линии линейной регрессии?

Наклон линии линейной регрессии — это численное значение, которое указывает на то, как два числовых значения(часто их называют переменными X и Y) зависят друг от друга, если точнее то одна из них зависимая переменная, а другая независимая.

К примеру, мы имеем информацию о возрасте людей и их среднем месячном доходе. Если мы будем вычислять для них наклон линии регрессии, он покажет есть ли связь между этими двумя параметрами.

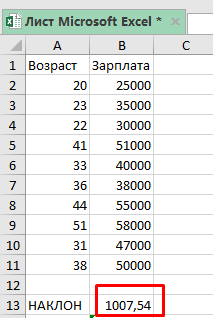
«Наклон» бывает положительный, либо отрицательный.

В данной ситуации мы имеем положительный наклон, это значит что есть положительная связь между возрастом людей и их зарплатой. Из этого значения наклона мы можем понять, что в среднем при увеличении возраста человека на 1 год, он зарабатывает на 1007,54 больше.

Кроме наклона линии, есть кое-что еще интересное, это функция ОТРЕЗОК.

Проще всего объяснить так:

Y = НАКЛОН*X + ОТРЕЗОК

В прошлом шаге мы рассчитали наклон линии, но чтобы вычислить значение Y, нам нужно знать еще и ОТРЕЗОК.

Я также продемонстрирую вам как вычислять и ОТРЕЗОК.

С помощью функции НАКЛОН

С помощью функции НАКЛОН можно рассчитать наклон линии, это стандартный способ.

Нам нужно просто указать значение независимой и зависимой переменных. Далее функция сделает все сама.

Составление формулы для функции НАКЛОН

Формула функции выглядит следующим образом:

=НАКЛОН(Y; X)  

Аргументы функции X и Y состоят из диапазона ячеек для которых нужно определить зависимость.

Не забывайте, что первым аргументом функции является Y, а вторым уже X. Если вы забудете об этом, то получите неправильный результат.

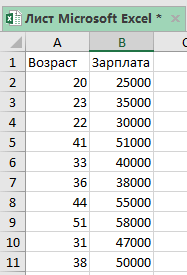
Допустим, у нас есть таблица, как на картинке. X в данном случае это возраст человека, а Y — его зарплата.

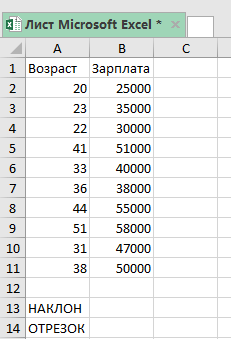
Конкретно для нашего примера, функция примет следующий вид:

=НАКЛОН(B2:B11;A2:A11)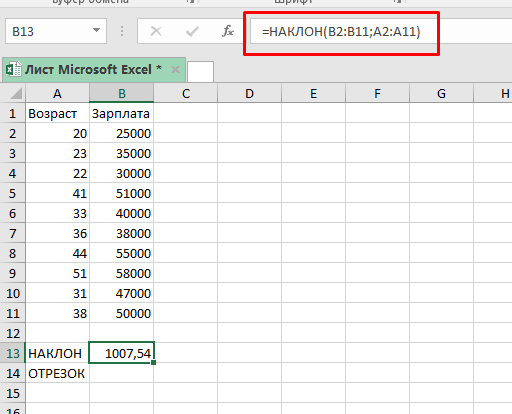  

Вычисление закончено. С помощью цифры, которую вывела наша функция, мы можем сказать, что в среднем, по этим данным, зарплата человека увеличивается на 1007,54 с каждым годом.

Расчет наклона тесно связан с еще одной важной величиной — ОТРЕЗКОМ.

Есть уравнение:

Y = Наклон*X + Отрезок

В нашем примере мы вычислили наклон линии, но чтобы знать значение Y для абсолютно любого X, мы должны знать еще и значение отрезка.

Вычислить его, мы можем с помощью специальной функции в Excel:

=ОТРЕЗОК(B2:B11;A2:A11)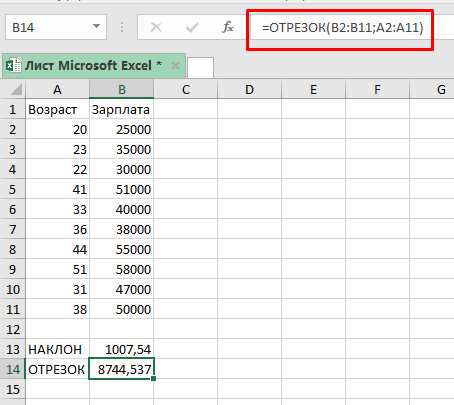  

Итак, уравнение, которое мы показывали выше, теперь, принимает такую форму:

Y = 1007,54*X + 8744,537

На данный момент, зная возраст человека, мы уже можем сказать, сколько будет его средняя зарплата. Подставим все значения, в наше уравнение:

Y =1007,54*37 + 8744,537  

Оба параметра, которые мы с вами научились вычислять, могут быть как положительными, так и отрицательными.

Инструкция по использованию функции НАКЛОН и ОТРЕЗОК

Мы с вами уже научили вычислять значения обеих функций, но есть кое-что о чем нужно знать:

• Аргументы обеих функций могут быть только числовыми.
• В этом случае, Excel не будет игнорировать нули, они участвуют во всех операциях.
• Важный момент, что в первом и втором аргументе должен быть одинаковый по количеству ячеек диапазон, иначе Excel будет возвращать вам ошибку.
• Также, в диапазоне ячеек должно быть больше, чем одна ячейка.

С помощью диаграммы

В случае если вам нравится использовать диаграммы, можно использовать эту функцию построения диаграммы в Excel чтобы вычислить НАКЛОН и ОТРЕЗОК.

Допустим, у нас есть все та же табличка с данными, которую мы использовали в первом способе.

Чтобы построить диаграмму, следуйте пошаговому руководству:

• Выделите диапазон ячеек, которые будут являться зависимыми и независимыми переменными .
• Щелкните на раздел «Вставка» в меню Excel.

• Выберите функцию «Вставить диаграмму».
• И укажите, что вам нужна точечная диаграмма.

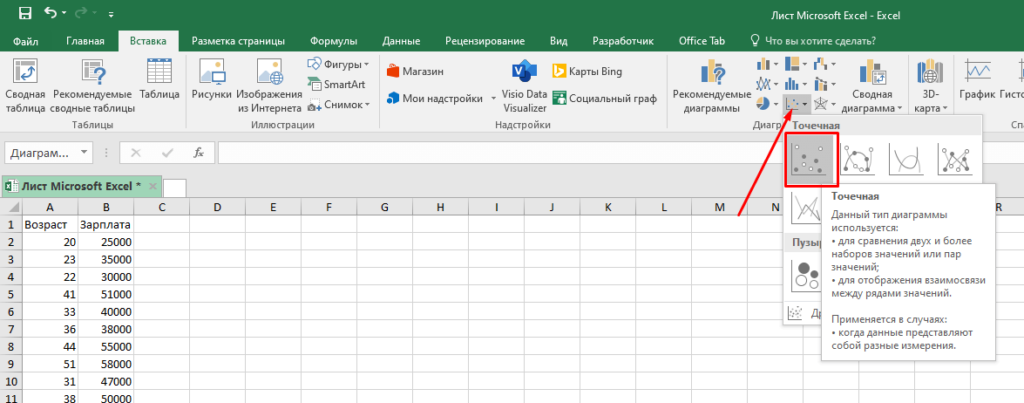
• Теперь Excel построит вам график, где будут соответствующие значения X и Y.

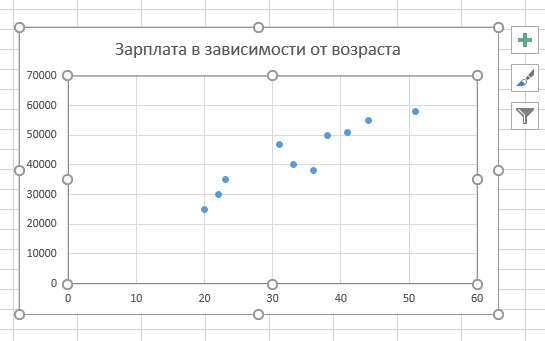
• Чтобы получить более детальную информацию, нажмите правой кнопкой мышки на любую из точек на графике. И щелкните на функцию «Добавить линию тренда». Откроется панель «Формат области построения».

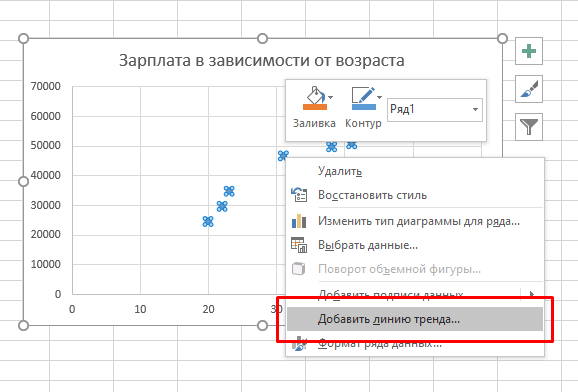
• На этой панели, вам нужно поставить галочку на параметре «показывать уравнение на диаграмме».

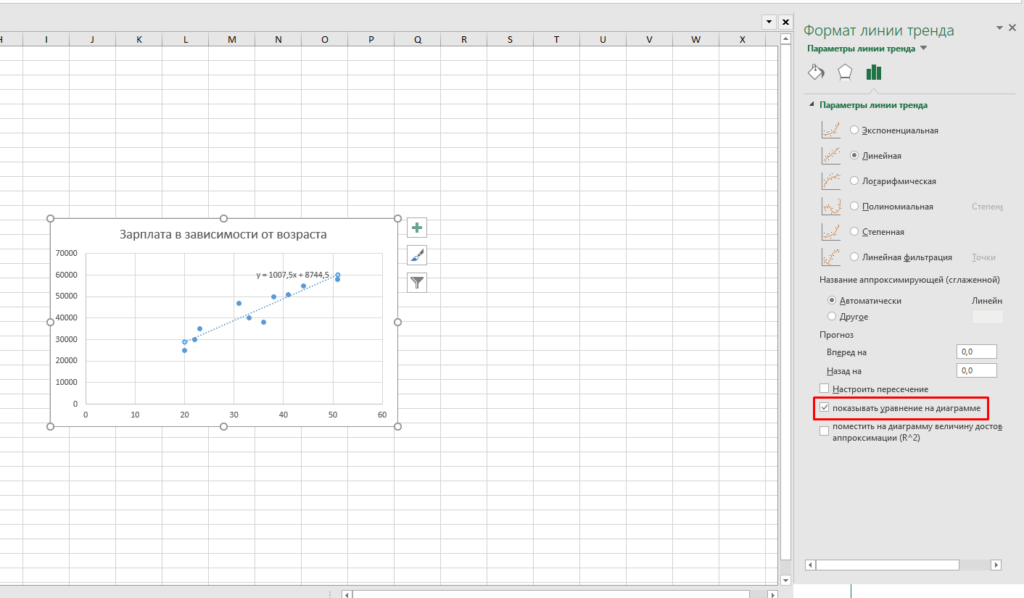
Теперь на этой диаграмме нам показывает полную информацию по наклону линии и отрезку.

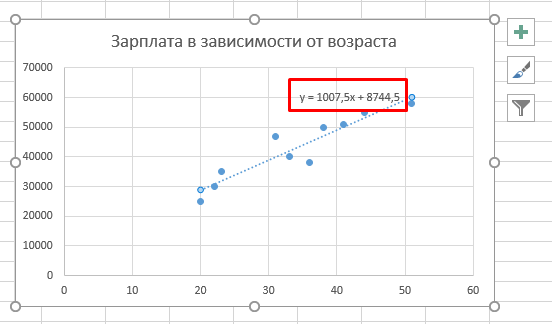
На графике, вы увидите точно такое же уравнение, которое мы составляли в прошлом способе.

y =1007,5x + 8744,5  

Вот:

• 1007,5 — наклон линии линейной регрессии
• 8744,5 — отрезок линии линейной регрессии

Если, в вашем случае, получилось положительное значение наклона, то вы увидите что линия направлена вверх, если же отрицательное, то вниз.

Что ж, вот и все. Оба этих способа довольно простые, но я все же рекомендую вам использовать диаграмму. Потому что на графике вы можете увидеть как располагаются имеющиеся точки данных.

И к тому же, я думаю, этот способ будет гораздо быстрее, чем вариант с помощью формул.

Это были 2 простых метода, как можно рассчитать параметры наклона линии регрессии и отрезка в Excel.

Надеюсь, вам помогло данное руководство!